
A evolução do número 1 e suas representações
Conheça um pouco da história do número 1, e como ele se transformou de um simples entalhe em um osso pré histórico no algarismo que conhecemos hoje.

Problema Resolvido: Conjuntos numéricos
Neste video, utilizamos o Diagrama de Venn e as operações com conjuntos para chegar à resposta do problema!

Divisão por Zero
Porque não podemos dividir um número por Zero? Assista e descubra!

De Arquimede a Pitágoras
Apresentamos aqui alguns dos nomes mais importantes da matemática e suas contribuições para os nossos estudos.

Problema Resolvido: Eleições
Veja como desenvolvemos a soma de números na casa da Centena de Milhar!

Problema Resolvido: Ônibus
A soma de horas tem suas peculiaridades. Neste video, mostramos como se faz a adição de horas para chegar à resposta do problema.

O equilíbrio na equação
Para manter os dois lados de uma equação equilibrados, tudo que é feito de um lado, deve ser feito do outro. Aqui usamos esta ideia para explicar porque 235 = 127 + x é equivalente à 235 - 127 = x.

Divisão por meio de frações
Como repartir a quantidade de grãos contida em 5 sacos de feijão por oito pessoas?

Segmentos em uma reta
Veja como um determinado segmento se comporta em uma reta.

Frações de Pizzas
Márcio e seu amigo comeram respectivamente 18 e 23 pedaços de pizza. Quem comeu mais pizzas? Atenção! é preciso saber de qual fração de uma pizza estamos falando em cada caso antes de responder à pergunta.

Multiplicação de frações
Como podemos transformar 5/8 e 7/12 em frações com o denominador 24?

Adição entre duas frações
Qual é a razão da expressão da soma de números racionais? Neste video, você vai descobrir como chegar a resposta para essa questão!

Mínimo Múltiplo Comum
O que é o MMC? Como chegamos a ele? Assista à explicação e veja alguns exemplos.

Problema Resolvido: Perímetro de um Terreno
Uma pessoa conseguiu medir dois quintos do perímetro do seu terreno e encontrou 15 metros e meio. Qual é o perímetro do terreno?

Leituras Decimais
Aprenda como podemos ler os números com duas casas decimais!

Problema Resolvido: Sala
Observe o a planta da sala de uma casa apresentada e calcule, quantos metros de madeira é preciso comprar para fazer o rodapé desta sala?

Quando não devemos prolongar uma divisão?
Uma professora tem 37 lápis para dividir igualmente entre 8 alunos. Quantos lápis ela dará a cada um?

A história do xadrez
Conheça a história do jogo de xadrez como contada por Malba Tahan em "O homem que calculava".

Propriedades de Potenciação
Veja como as propriedades das potências são desenvolvidas.

Expressões com potências: Exemplo 1
Como desenvolver uma expressão utilizando-se das propriedades da potenciação? Veja este exemplo.

Expressões com potências: Exemplo 2
Veja mais este exemplo sobre o uso das propriedas da potenciação para resolver uma expressão.

Área, Volume e Radiciação
Dado a área, qual é o valor da lateral de um quadrado? Ou de um cubo? Podemos responder estas questões sabendo mais sobre radiciação.
Números Fracionários e os egípcios
E quando temos um grupo de pessoas e só é possível que cada uma delas fique com uma parte de um objeto a ser dividido?
Precisamos recorrer ao método de particionar o que temos entre todos, buscando a igualdade. Para isso, usamos a divisão, e também um novo conjunto numérico: o conjunto dos números racionais fracionários.
pouco sobre o sistema numérico egípcio:
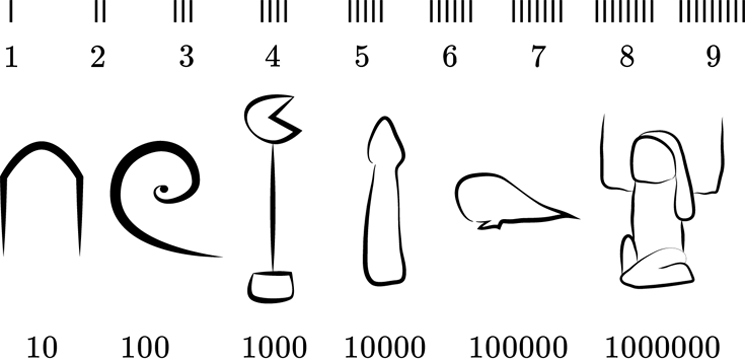
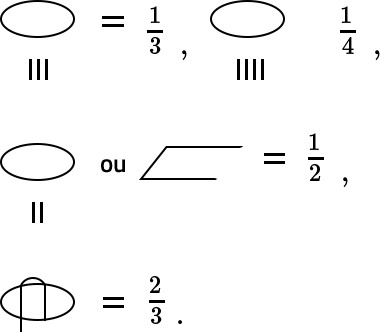
Divisão por meio de frações
Como repartir a quantidade de grãos contida em 5 sacos de feijão por oito pessoas?
